[파이썬] 파이썬 데이터 사이언스 핸드북 정리(2일차)
파이썬 데이터 사이언스 핸드북 -제이크 밴더플래스- -위키북스- P73 ~ P110까지 (NumPy에 관한 챕터2 끝)
전체 내용 리마인드겸 짧게 요약 (내가 보기 좋게..)
- 브로드캐스팅은 배열 맞지 않는거 규칙으로써 맞추는것(중앙 정렬할 때 썼음, X_centered = X - Xmean 할때)
- 부울 연산자(T/F)로 요소 갯수세고(예:np.sum(x<6)
- 마스크로 부울 사용하기(x[x <5]])
- 팬시 인덱싱 : 어떤 요소만 빼낼때, 내가 배열을 정해서 빼낼수 있다.(=인덱싱 할수 있다.)
- 결합 인덱싱 : 팬시 + 단순 (예 : X[2, [2, 0, 1]] <- 이런 느낌으로 단일과 배열로 합친다는 얘기임
- 솔팅하는거 : 알고리즘으로 가능하나 내장 함수 np.sort와 np.argsort 사용
- 파티션 나누기(일부만 솔팅하는거) : 이거 k 최근접 이웃 알고리즘 짤때, 굳이 다 솔팅 할 필요없이 몇개만 내 주변에 있는지 확인하고 넘어가면 되기 때문
배열 연산 : 브로드캐스팅
브로드캐스팅은 단지 다른 크기의 배열에 이항 유니버설 함수를 적용하기 위한 규칙
브로드캐스팅 소개
import numpy as np
a = np.array([0, 1, 2])
b = np.array([5, 5, 5])
a + b
array([5, 6, 7])
# 더 쉽게 할 수 있다.
a + 5
array([5, 6, 7])
M = np.ones((3, 3))
M
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
M + a
array([[1., 2., 3.],
[1., 2., 3.],
[1., 2., 3.]])
여기서 1차원 a는 M의 형상에 맞추기 위해 두버내 차원까지 브로드캐스팅(확장)된다.
# 두 배열 모두 브로드캐스팅 하는 경우
a = np.arange(3)
b = np.arange(3)[:, np.newaxis]
print(a)
print(b)
[0 1 2]
[[0]
[1]
[2]]
a + b
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])
공통 형상을 맞추기위해 a와 b 모두 확장된것을 볼 수 있다.
브로드캐스팅 규칙
- 규칙 1 : 두 배열의 차원수가 다른면 더 작은 수의 차원을 가진 배열 형상의 앞쪽(왼쪽)을 1로 채운다.
- 규칙 2 : 두 배열의 형상이 어떤 차원에서도 일치하지 않는다면 해당 차원의 형상이 1인 배열이 다른 형상과 일치하도록 늘어난다.
- 규칙 3 : 임의의 차원에서 크기가 일치하지 않고 1도 아니라면 오류가 발생한다.
브로드캐스팅 예제 1
M = np.ones((2, 3))
a = np.arange(3)
print(M)
print(a)
[[1. 1. 1.]
[1. 1. 1.]]
[0 1 2]
# 규칙에 맞춰서 차원 일치시켜서 나온다. 나머지 예시들은 나중에 해보도록 하자.
M + a
array([[1., 2., 3.],
[1., 2., 3.]])
실전 브로드캐스팅
배열을 중앙 정렬하기
앞에서 ufunc을 사용하면 루프를 사용하지 않아도 되고, 브로드캐스팅은 이 능력을 확장
흔히 볼 수 있는 예는 데이터 배열을 중앙 정렬하는 것이다.
(쉽게 말하면 평균 0 으로 중간 정렬할때, 각 열의 평균으로 센터화 할때 배열이 안맞는데 이거를 브로드캐스팅으로 맞춰준다는 얘기이다.
X = np.random.random((10, 3))
Xmean = X.mean(0)
Xmean
array([0.41956243, 0.56206976, 0.54391253])
X_centered = X - Xmean
X_centered.mean(0)
array([-4.44089210e-17, 3.33066907e-17, -3.33066907e-17])
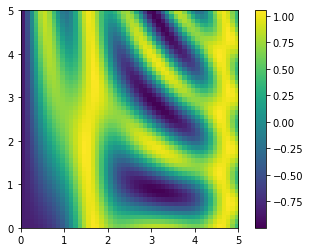
2차원 함수 플로팅 하기
브로드캐스팅은 2차원 함수를 기반으로 이미지를 그릴 떄도 매우 유용하다.
# x와 y는 0에서 5까지 50단계로 나눈 배열
x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 50)[:, np.newaxis]
z = np.sin(x) ** 10 + np.cos(10 + y * x)*np.cos(x)
%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(z, origin='lower', extent=[0, 5, 0, 5],
cmap='viridis')
plt.colorbar();
비교, 마스크, 부울 로직
Numpy 배열 내의 값을 검사하고 조직하는 데 부울 마스크를 사용하는 법을 배움
마스킹은 특정 기준에 따라 배열의 값을 추출, 수정, 계산할 때 사용
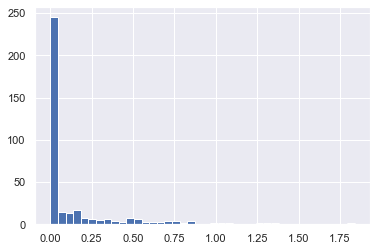
예제 : 비온 날 세기
import numpy as np
import pandas as pd
# Pandas를 이용해 인치 단위의 강수량 데이터를 NUmpy 배열로 추출
rainfall = pd.read_csv('data/Seattle2014.csv')['PRCP'].values
inches = rainfall / 254 # 1/10mm->inches
inches.shape
(365,)
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn; seaborn.set() # 플롯 형식 설정
plt.hist(inches, 40);
ufunc으로서의 비교 연산자
x = np.array([1, 2, 3, 4, 5])
x < 3
array([ True, True, False, False, False])
x != 3
array([ True, True, False, True, True])
(2 * x) == (x ** 2)
array([False, True, False, False, False])
# 2차원 예제
rng = np.random.RandomState(0)
x = rng.randint(10, size = (3, 4))
x
array([[5, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6]])
x<6
array([[ True, True, True, True],
[False, False, True, True],
[ True, True, False, False]])
## 부울 배열로 작업하기
print(x)
[[5 0 3 3]
[7 9 3 5]
[2 4 7 6]]
요소 개수 세기
# 6보다 작은 값은 몇 개일까?
np.count_nonzero(x < 6)
8
np.sum(x<6)
8
# 각 행에 6보다 작은 값이 몇 개 일까?
np.sum(x < 6, axis = 1)
array([4, 2, 2])
# 8보다 큰 값이 하나라도 있는가?
np.any(x > 8)
True
# 모든 값이 10보다 작은가?
np.all(x < 10)
True
# 각 행의 모든 값이 8보다 작은가?
np.all(x < 8, axis = 1)
array([ True, False, True])
부울 연산자
np.sum((inches > 0.5) & (inches < 1)) # sum 쓴 이유는 True false 로 나오니까 그 수를 세면 갯수랑 같음
29
print("Number days without rain: ", np.sum(inches == 0))
Number days without rain: 215
마스크로서의 부울 배열 (예시:x[x<5] <- 마스킹 연산)
마스크로 사용해 데이터 자체의 특정 부분 집합으을 선택하는 패턴이 더 강력하다.
x
array([[5, 0, 3, 3],
[7, 9, 3, 5],
[2, 4, 7, 6]])
x < 5
array([[False, True, True, True],
[False, False, True, False],
[ True, True, False, False]])
# 마스크 배열이 True인 위치에 있는 모든 값으로 채워진 1차원 배열을 만듬
x[x<5]
array([0, 3, 3, 3, 2, 4])
# 비가 온 모든 날에 대한 마스크 생성
rainy = (inches > 0)
# 여름에 해당하는 날
summer = (np.arange(365) - 172 < 90) & (np.arange(365) - 172 > 0)
print("Median precip on rainy days in 2014 (inches): ", np.median(inches[rainy]))
Median precip on rainy days in 2014 (inches): 0.19488188976377951
팬시 인덱싱
한번에 여러 배열 요소에 접근하기 위해 인덱스의 배열을 전달
import numpy as np
rand = np.random.RandomState(42)
x = rand.randint(100, size = 10)
print(x)
[51 92 14 71 60 20 82 86 74 74]
# 세 개의 다른 요소에 접근하고자 할떄
[x[3], x[7], x[2]]
[71, 86, 14]
ind = [3, 7, 4]
x[ind]
array([71, 86, 60])
# 팬시 인덱싱을 이용하면 결과의 형상이 인덱싱 대상 배열 형상이 아니라, 인덱스 배열의 형상으로 반영된다.
# 쉽게 말하면 원 데이터의 행렬이 아니라 인덱스로 내가 정해주는 행렬로 나옴
ind = np.array([[3, 7],
[4, 5]])
x[ind]
array([[71, 86],
[60, 20]])
X = np.arange(12).reshape((3, 4))
X
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
row = np.array([0, 1, 2])
col = np.array([2, 1, 3])
X[row, col]
array([ 2, 5, 11])
# 팬시 인덱싱에서 인덱스 쌍을 만드는 것도 브로드캐스팅 규칙을 따른다.
X[row[:, np.newaxis], col]
array([[ 2, 1, 3],
[ 6, 5, 7],
[10, 9, 11]])
row[:, np.newaxis]
array([[0],
[1],
[2]])
col
array([2, 1, 3])
# 잘 보면 이렇게 브로드 캐스팅이 된 것을 볼 수 있다
row[:, np.newaxis] * col
array([[0, 0, 0],
[2, 1, 3],
[4, 2, 6]])
결합 인덱싱
다른 인덱싱 방식과 결합 할수 있다.
print(X)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
# 팬시 인덱스와 단순 인덱스를 결합 할 수 있다.
X[2, [2, 0, 1]]
array([10, 8, 9])
X[1:, [2, 0 , 1]]
array([[ 6, 4, 5],
[10, 8, 9]])
mask = np.array([1, 0 , 1, 0], dtype = bool)
X[row[:, np.newaxis], mask]
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
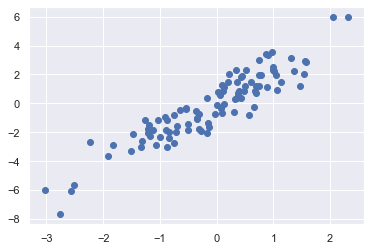
예제 : 임의의 점 선택하기
mean = [0, 0]
cov = [[1,2],
[2, 5]]
X = rand.multivariate_normal(mean, cov, 100)
X.shape
(100, 2)
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn; seaborn.set() # 플롯 스타일 설정
plt.scatter(X[:, 0], X[:, 1]);
indices = np.random.choice(X.shape[0], 20, replace=False)
indices
array([22, 26, 36, 19, 1, 56, 2, 67, 50, 7, 38, 35, 98, 10, 13, 27, 47,
93, 89, 54])
selection = X[indices] # 여기에 팬시 인덱싱 사용
selection.shape
(20, 2)
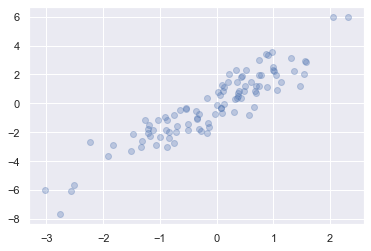
# 전체 점 가운데 임의로 20개를 선택한 PLOT 그림
plt.scatter(X[:, 0], X[:, 1], alpha=0.3)
plt.scatter(selection[:, 0], selection[:, 1],
facecolor='none', s=200)
<matplotlib.collections.PathCollection at 0x15d51cbb408>
팬시 인덱싱으로 값 변경하기
배열의 일부에 접근해서 수정하는데도 사용할 수 있다.
x = np.arange(10)
i = np.array([2, 1, 8, 4])
x[i] = 99
print(x)
[ 0 99 99 3 99 5 6 7 99 9]
x[i] -= 10
print(x)
[ 0 89 89 3 89 5 6 7 89 9]
# 반복되는 인덱스는 예상치 못한 결과를 초래할 수 있음
x = np.zeros(10)
x[[0, 0]] = [4, 6]
print(x)
# x[0] = 4가 할당되고 6이 할당되서 6만 갖는다.
[6. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
i = [2, 3, 3, 4, 4, 4]
x[i] += 1
x
# 왜 x[3]이 2가 안되었으며, x[4]가 3이 안되었을까?
# 증가가 아니라 할당 개념인데.. 사실 잘은 모르겠다.
array([6., 0., 2., 2., 2., 0., 0., 0., 0., 0.])
# 여튼 이런 경우에는
x = np.zeros(10)
np.add.at(x, i, 1)
print(x)
# 이렇게 해야한다. 어렵다..이해하기
[0. 0. 1. 2. 3. 0. 0. 0. 0. 0.]
예제 : 데이터 구간화
# 히스토그램 노가다로 만들기..(노 필요)
np.random.seed(42)
x = np.random.randn(100)
# 직접 히스토그램 계산하기
bins = np.linspace(-5, 5, 20)
counts = np.zeros_like(bins) # bins배열 모양의 0으로 된 배열 만듬
# 각 x에 대한 적절한 구간 찾기
i = np.searchsorted(bins, x)
# 각 구간에 1 더하기
np.add.at(counts, i , 1)
# 결과 플로팅하기
plt.plot(bins, counts, linestyle='steps')
d:\python_study\python_handbook\venv\lib\site-packages\ipykernel_launcher.py:3: MatplotlibDeprecationWarning: Passing the drawstyle with the linestyle as a single string is deprecated since Matplotlib 3.1 and support will be removed in 3.3; please pass the drawstyle separately using the drawstyle keyword argument to Line2D or set_drawstyle() method (or ds/set_ds()).
This is separate from the ipykernel package so we can avoid doing imports until
[<matplotlib.lines.Line2D at 0x15d531f2a08>]
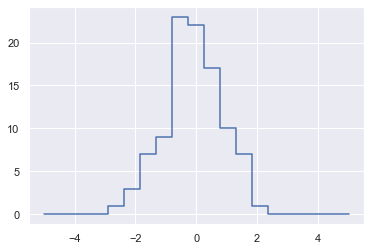
# 물론 히스토그램을 그릴때마다 이렇게 하는것은 바보 같다....괜히 연구했네
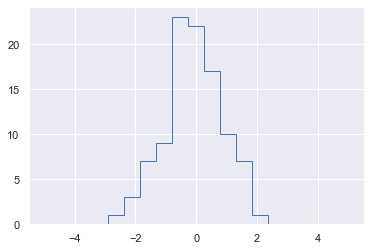
plt.hist(x, bins, histtype='step')
(array([ 0., 0., 0., 0., 1., 3., 7., 9., 23., 22., 17., 10., 7.,
1., 0., 0., 0., 0., 0.]),
array([-5. , -4.47368421, -3.94736842, -3.42105263, -2.89473684,
-2.36842105, -1.84210526, -1.31578947, -0.78947368, -0.26315789,
0.26315789, 0.78947368, 1.31578947, 1.84210526, 2.36842105,
2.89473684, 3.42105263, 3.94736842, 4.47368421, 5. ]),
<a list of 1 Patch objects>)
배열 정렬
이번 절에서는 NumPy 배열의 값을 정렬하는 알고리즘을 다룸
# 예를 들어 간단한 선택정렬은 리스트의 최솟값을 반복적으로 찾아서 리스트가 정렬될 때까지 값을 교환한다.
import numpy as np
def selection_sort(x) :
for i in range(len(x)) :
swap = i + np.argmin(x[i:])
(x[i], x[swap]) = (x[swap], x[i])
return x
x = np.array([2, 1, 4, 3, 5])
selection_sort(x)
array([1, 2, 3, 4, 5])
NumPy의 빠른 정렬 : np.sort 와 np.argsort
x = np.array([2, 1, 4, 3, 5])
np.sort(x)
array([1, 2, 3, 4, 5])
# 그자리에서 바로 배열하는 게 좋으면
x.sort()
print(x)
[1 2 3 4 5]
# 정렬된 요소를 인덱스로 반환하는 argsort도 있다.
x = np.array([2, 1, 4, 3, 5])
i = np.argsort(x)
print(i)
[1 0 3 2 4]
x[i]
array([1, 2, 3, 4, 5])
행이나 열 기준으로 정렬하기
rand = np.random.RandomState(42)
X = rand.randint(0, 10, (4,6))
print(X)
[[6 3 7 4 6 9]
[2 6 7 4 3 7]
[7 2 5 4 1 7]
[5 1 4 0 9 5]]
# X의 각 열을 정렬
np.sort(X, axis=0)
array([[2, 1, 4, 0, 1, 5],
[5, 2, 5, 4, 3, 7],
[6, 3, 7, 4, 6, 7],
[7, 6, 7, 4, 9, 9]])
# X의 각 행을 정렬
np.sort(X, axis=1)
array([[3, 4, 6, 6, 7, 9],
[2, 3, 4, 6, 7, 7],
[1, 2, 4, 5, 7, 7],
[0, 1, 4, 5, 5, 9]])
부분 정렬: 파티션 나누기
약간 어디다 쓰는지 모르겠음
x = np.array([7, 2, 3, 1, 6, 5, 4])
np.partition(x, 3)
# 왼쪽에 3개 가장 작은거 나온다.
array([2, 1, 3, 4, 6, 5, 7])
np.partition(X, 2, axis=1)
array([[3, 4, 6, 7, 6, 9],
[2, 3, 4, 7, 6, 7],
[1, 2, 4, 5, 7, 7],
[0, 1, 4, 5, 9, 5]])
예제 : k 최근접 이웃 알고리즘
argsort함수를 어떻게 사용하는지 볼라고함
X = rand.rand(10, 2)
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn; seaborn.set() # 플롯 스타일링
plt.scatter(X[:, 0], X[:, 1], s=100);
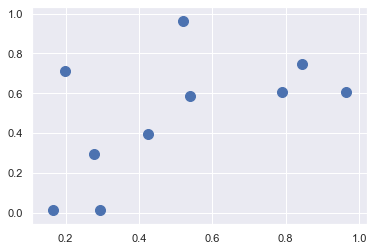
# 이제 각 쌍의 점 사이의 거리를 계싼함
dist_sq = np.sum((X[:,np.newaxis,:] - X[np.newaxis,:,:]) ** 2, axis=-1)
# 브로드캐스팅 규칙이 익숙하지 않는 독자라면 이 코드를 봐야한다 (나!!)
# 각 쌍의 점 사이의 좌표 차이를 계산
differences = X[:, np.newaxis, :] - X[np.newaxis, :, :]
differences.shape
(10, 10, 2)
sq_differences = differences ** 2
sq_differences.shape
(10, 10, 2)
dist_sq = sq_differences.sum(-1)
dist_sq.shape
(10, 10)
dist_sq.diagonal()
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
nearest = np.argsort(dist_sq, axis=1)
print(nearest)
[[0 2 1 8 9 3 6 4 7 5]
[1 9 3 2 0 6 8 4 7 5]
[2 6 9 1 8 0 4 3 7 5]
[3 9 1 2 0 6 4 8 7 5]
[4 6 7 5 2 8 9 0 1 3]
[5 7 4 6 2 8 9 3 1 0]
[6 4 2 8 7 9 5 1 0 3]
[7 5 4 6 2 8 9 3 1 0]
[8 2 6 0 4 9 1 5 7 3]
[9 1 3 2 6 0 4 8 7 5]]
# 눈치 챗겠지만 각점의 가장 가까운 이웃은 자기 자신이기때문에 첫열은 0~9 순서이다.
# 여기서는 가장 가까운k이웃만 구하면 된다. 그래서 각행을 파티션으로 나눠
# 가장 작은 k+1개의 제곱 거리가 먼저 오고 그 보다 큰 거리의 요소를 배열의 나머지 위치에 채워지게만 하면된다.
# 그 작업은 np.argpartition 함수로 할수 있다.
K = 2
nearest_partition = np.argpartition(dist_sq, K+1, axis=1)
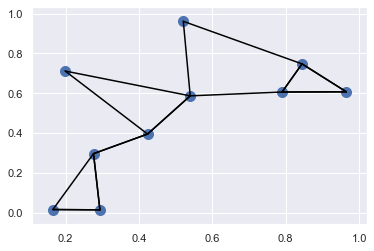
plt.scatter(X[:,0], X[:,1], s=100)
# 각 점을 두개의 가장 가까운 이웃과 선으로 이음
K=2
for i in range(X.shape[0]) :
for j in nearest_partition[i, :K+1]:
# X[i]부터 X[j]까지 선으로 이음
# zip 매직 함수를 이용함
plt.plot(*zip(X[j], X[i]), color='black')
구조화된 데이터 : NumPy의 구조화된 배열
대체로 데이터는 동종의 값의 배열을 잘 표현할 수 있지만 아닌 경우도 있다. 이 절에서는 NumPy에서 복합적인 이종 데이터를 효율적으로 저장하기 위한 구조화된 배열과 레코드 배열에 관해 설명하겠다.
# 다양한 종류의 데이터(이름, 나이, 몸무게)를 저장하고 싶다고하자.
name = ['Alice', 'Bob', 'Cathy', 'Doug']
age = [25, 45, 37, 19]
weight = [55.0, 85.5, 68.0, 61.5]
# 이방식은 다소 어설프다. 이 세 배열이 서로 연관되어 있음을 알 수가 없다.
# 이 데이터를 단일 구조에 저장할 수 있다면 더 자연스러울 것이다.
x = np.zeros(4, dtype=int)
# 구조화된 배열을 위해 복합 데이터 타입 사용
data = np.zeros(4, dtype={'names':('name', 'age', 'weight',),
'formats':('U10', 'i4', 'f8')}) # 32비트 정수 등 이런거
print(data.dtype)
[('name', '<U10'), ('age', '<i4'), ('weight', '<f8')]
# 빈 컨테이너 배열을 만들었으니 이제 값 리스트를 채우면 된다.
data['name'] = name
data['age'] = age
data['weight'] = weight
print(data)
[('Alice', 25, 55. ) ('Bob', 45, 85.5) ('Cathy', 37, 68. )
('Doug', 19, 61.5)]
# 값을 인덱스나 이름으로 참조
# 전체 이름 가져오기
data['name']
array(['Alice', 'Bob', 'Cathy', 'Doug'], dtype='<U10')
data[0]
('Alice', 25, 55.)
# 부울 마스킹으로 나이 필터 넣음
data[data['age'] < 30]['name']
array(['Alice', 'Doug'], dtype='<U10')
구조화된 배열 만들기
딕셔너리, 숫자타입, 튜플의 리스트 등등 할수 있다.(넘어가자)
